Введение
Одна из наиболее важных прикладных областей принятия решений, приносящих наибольшую экономическую выгоду - это обеспечение качества продукции, основанное на применении статистического моделирования.
Руководители и специалисты промышленных предприятий хотят не только выжить, но и выиграть в борьбе с конкурентами. Более частными задачами, которые они хотят решить, обычно являются:
- выйти на международный рынок;
- поднять качество продукции до японского уровня;
- полностью ликвидировать рекламации, и т.д.
Ключевой фактор для решения этих задач является контроль качества продукции. Все руководители и специалисты промышленных предприятий хорошо знают термины: "сертификация", "международные стандарты ИСО (т.е. разработанные International Standardization Organization - Международной организацией по стандартизации, сокращенно ISO, по-русски - ИСО) серии 9000 по системам качества". Под этими терминами скрывается прежде всего применение современных методов принятия решений на основе статистического моделирования. На Западе (США) и на Востоке (Япония) это - аксиома. Вот типичное высказывание японского менеджера и инженера: "Методы статистики - именно то средство, которое необходимо изучить, чтобы внедрить управление качеством. Они - наиболее важная составная часть комплексной системы всеобщего управления качеством на фирме. В японских корпорациях все, начиная от председателя Совета Директоров и до рядового рабочего в цехе, обязаны знать хотя бы основы статистических методов". Так считает Каору Исикава, президент промышленного института Мусаси, заслуженный профессор Токийского университета.
Постановка задачи
Контролем качества продукции обычно занимается отдел технического контроля (ОТК) предприятия. Есть различные виды контроля:
- входной контроль,
- приемочный контроль (готовой продукции),
- контроль при передаче полуфабрикатов и комплектующих из цеха в цех.
Среди способов контроля выделяют два наиболее часто встречающихся: сплошной контроль всех изделий подряд и выборочный, когда о качестве партии продукции судят по результатам контроля некоторой части - выборки.
Данная работа посвящена первому способу контроля, так как он подходит, как и к относительно простым и дешевым изделиям (например, бутылкам), так и к технологически сложным и дорогостоящим (например, ракетоносителям).
Кроме того есть изделия, которые можно контролировать только выборочно, например, чтобы проверить качество спички - надо чиркнуть ею. Загорится - должное качество, не загорится - брак. Но повторно однажды зажженную спичку использовать уже нельзя. Поэтому партию спичек можно контролировать только выборочно. Такими же изделиями являются консервы, лампочки, патроны и т.п. Т.е. при разрушающем контроле необходимо пользоваться выборочными методами и судить о качестве партии продукции по результатам контроля её части - выборки.
Выборочные методы контроля могут применяться и из экономических соображений, когда стоимость контроля высока по сравнению со стоимостью изделия. Например, вряд ли целесообразно визуально проверять качество каждой скрепки в каждой коробке.
Контроль качества продукции на основе биномиальной модели
В связи с переходом промышленности на массовое изготовление изделий за последние пятьдесят-шестьдесят лет резко увеличился интерес к вопросам проверки качества изделий? входящих в принимаемую партию. Появилась глубокая по содержанию и значительная по своим практическим применениям теория статистических методов приемочного контроля, основанная на широком использовании теории вероятностей. Первым шагом относящимся к этому кругу идей по-видимому следует считать одну из задач рассмотренных Симпсоном в книге “Природа и законы случая”. Вот формулировка этой задачи: имеется данное число вещей различного сорта n1 вещей первого, n2 второго. Наудачу берутся n вещей. Найти вероятность того, что при этом будет взято m1 вещей первого сорта, m2 вещей второго и т.д.
Спустя сто с небольшим лет, к этой задаче вновь вернулся Остроградский в работе “Об одном вопросе, касающемся вероятностей”. В математическом отношении это произведение Остроградского не представляет большого интереса, но глубокое понимание самой практической задачи заслуживает внимания. По-видимому, в этом отношении он имеет приоритет перед всеми исследователями. Во всяком случае Cимпсон практических следствий из своих подсчетов не делал, а Остроградский вычислил и необходимые для практических применений таблицы. Приведем подлинные слова Остроградского: “В сосуде имеются белые и черные шары, общее количество которых нам известно, но мы не знаем, сколько из них какого цвета. Мы извлекаем некоторое количество шаров, подсчитав, сколько из них белых и сколько черных, снова кладем в сосуд. Требуется определить вероятность того, что общее число белых не выходит, из наперед заданных пределов. Или, лучше сказать, мы ищем зависимость между этой вероятностью и пределами, о которых идет речь”. Важность этого вопроса возрастает в разы, когда в роли, извлекающей шары, выступает поставщик продукции. Перед поставщиками часто стоят такого рода задачи. Для них шары, содержащиеся в cосуде, представляют получаемые предметы, белые, например "предметы приемлемые”, как удовлетворяющие определенным условиям, а черные "неприемлемые”. Таким образом, решение такой задачи позволяет поставщику свести приблизительно к двадцатой доле часто очень утомительную механическую работу, используя выборочный способ контроля, а не проверять изделия поштучно.
Общее число шаров в урне известно, но неизвестен ее состав. Его и следует оценить по выборке, взятой из урны наудачу. Для этой цели Остроградский использует формулы Байеса. Однако его рассуждения базируются на одном предположении, которое вызывает серьезные возражения, поскольку в реальной практике не может встретиться. Именно, он предположил, что если n - общее число шаров в урне, то одинаково вероятны все гипотезы о распределении среди них белых и черных шаров, т.е. что одинаково вероятны все следующие n + 1 предположения о числе белых шаров 0, 1, 2, ..., n. В действительности ближе к истине предположение, которое используется теперь в задачах приемочного статистического контроля качества. Предполагается, что имеется причина, в силу которой каждое изделие может оказаться бракованным с вероятностью p. Для хорошо организованного производства p должно быть малым и практически неизменным. Если же технологический процесс налажен плохо, то вероятность p зависит от времени и может достигать большой величины.
Но очевидно, что в этом случае статистический контроль не может принести пользы. Если же p мало и постоянно, то вероятность среди n изделий встретить m бракованных задается формулой Бернулли:
где q = 1-p;
p – вероятность брака;
m – количество бракованных изделий;
n – общее число изделий в партии;
Статистические методы приемочного контроля получили особенно бурное развитие в годы Второй мировой войны, поскольку было необходимо принимать огромные партии однородной продукции, а проверять ее сплошь не было возможностей по ряду причин, из которых укажем лишь на следующие: для некоторых видов продукции Проверка равносильна уничтожению рабочих свойств изделия (фотобумага, взрыватели и т.д.); для сплошной проверки требовалось такое количество рабочей силы и рабочего времени, что ни то, ни другое не могло быть обеспечено в условиях военного времени. Нет возможности здесь перечислить даже основные этапы развития теории статистических методов приемочного контроля. Большое число исследователей работали над различными проблемами этой тематики и внесли в ее развитие крупный вклад. Из отечественных ученых заслуживают быть отмеченными А. Н. Колмогоров, В. И. Романовский, С. Х. Сираждинов, Ю. К. Беляев и др. В период Великой Отечественной войны огромное внимание было уделено разработке методов управления качеством продукции в процессе производства. Это весьма важное направление работы, поскольку оно должно не просто разбраковывать изготовленную продукцию, но своевременно вмешиваться в производственный процесс и не допускать изготовления некачественной продукции. Именно к этому и должно стремиться любое производство.
Сравнение биномиальной и гипергеометрической модели
Выборочный контроль, построенный на научной основе, т.е. исходящий из теории вероятностей и математической статистики, называют статистическим контролем. Предпринимателя и менеджера выборочный контроль может интересовать не только в связи с качеством продукции, но и в связи, например, с контролем экологической обстановки, поскольку зафиксированные государственными органами экологические нарушения влекут штрафы и иные "неприятные" последствия. Обсудим основные подходы статистического контроля.
При статистическом контроле решение о генеральной совокупности – об экологической обстановке в данном регионе или о партии продукции - принимается по выборке, состоящей из некоторого количества единиц (единиц экологического контроля или единиц продукции). Следовательно, выборка должна представлять партию, т.е. быть репрезентативной (представительной). Как эти слова понимать, как проверить репрезентативность? Ответ может быть дан лишь в терминах вероятностных моделей выборки.
Наиболее распространенными являются две вероятностные модели—биномиальная и гипергеометрическая. В биномиальной модели предполагается, что результаты контроля n единиц можно рассматривать как совокупность n независимых одинаково распределенных случайных величин Х1, Х2,....,Хn , где Хi = 1, если i‑ое измерение показывает, что есть нарушение, т.е. превышено ПДК (предельная норма концентрации) или i‑ое изделие дефектно, и Хi= 0, если это не так. Тогда число Х превышений ПДК или дефектных единиц продукции в партии равно
Х= Х1+ Х2+...+ Хn .(1)
Из формулы (1) и Центральной Предельной Теоремы теории вероятностей вытекает, что при увеличении объема выборки n распределение Х сближается с нормальным распределением. Известно, что распределение Х имеет вид
Р( Х= k) = Cnk pk (1—p)n-k , (2)
где Cnk - число сочетаний из n элементов по k, а p —уровень дефектности (в другой предметной области - доля превышений ПДК в генеральной совокупности), т.е. p = Р( Хi= 1). Формула (2) задает так называемое биномиальное распределение.
Гипергеометрическое распределение соответствует случайному отбору единиц в выборку. Пусть среди N единиц, составляющих генеральную совокупность, имеется D дефектных. Случайность отбора означает, что каждая единица имеет одинаковые шансы попасть в выборку. Мало того, ни одна пара единиц не должна иметь при отборе в выборку преимущества перед любой другой парой. То же самое —для троек, четверок и т.д. Это условие выполнено тогда и только тогда, когда каждое из сочетаний по n единиц из N имеет одинаковые шансы быть отобранным в качестве выборки. Вероятность того, что будет отобрано заранее заданное сочетание, равна, очевидно, CNn.
Отбор случайной выборки согласно описанным правилам организуют при проведении различных лотерей. Пусть Y —число дефектных единиц в случайной выборке, организованной таким образом. Известно, что тогда P (Y = k) – гипергеометрическое распределение, т.е.
Замечательный математический результат состоит в том, что биномиальная и гипергеометрическая модели весьма близки, когда объем генеральной совокупности (партии) по крайней мере в 10 раз превышает объем выборки. Другими словами, можно принять, что
Р( Х = k) = P ( Y = k ), (4)
если объем выборки мал по сравнению с объемом партии. При этом в качестве p в формуле (4) берут D/N. Близость результатов, получаемых с помощью биномиальной и гипергеометрической моделей, весьма важна с философской точки зрения. Дело в том, что эти модели исходят из принципиально различных философских предпосылок. В биномиальной модели случайность присуща каждой единице - она с какой-то вероятностью дефектна, а с какой-то - годна. В то же время в гипергеометрической модели качество определенной единицы детерминировано, задано, а случайность проявляется лишь в отборе, вносится контроллером или экономистом при составлении выборки.
Соотношение (4) показывают, что во многих случаях нет необходимости принимать решения о выборе модели, поскольку обе модели дают близкие численные результаты. Отличия проявляются при обсуждении вопроса о том, какую выборку считать представительной. Является ли таковой выборка, составленная из 20 изделий, лежащих сверху в первом вскрытом ящике? В биномиальной модели - да, в гипергеометрической - нет.
Биномиальная модель легче для теоретического изучения. Однако при реальном контроле лучше формировать выборку, исходя из гипергеометрической модели. Это делают, выбирая номера изделий (для включения в выборку) с помощью датчиков псевдослучайных чисел на ЭВМ или с помощью таблиц псевдослучайных чисел. Алгоритмы формирования выборки встраивают в современные программные продукты по статистическому контролю.
Планы статистического контроля и правила принятия решений
Под планом статистического контроля понимают алгоритм, т.е. правила действий, на входе при этом—генеральная совокупность (партия продукции), а на выходе—одно из двух решений: «принять партию» либо «забраковать партию». Рассмотрим несколько примеров.
Одноступенчатые планы контроля (n,c): отобрать выборку объема n; если число дефектных единиц в выборке X не превосходит c, то партию принять, в противном случае забраковать. Число с называется приемочным.
Частные случаи: план (n,0) —партию принять тогда и только тогда, когда все единицы в выборке являются годными; план (n,1) - партия принимается, если в выборке все единицы являются годными или ровно одно - дефектное, во всех остальных случаях партия бракуется.
Двухступенчатый план контроля (n,a,b) + (m,c): отобрать первую выборку объема n; если число дефектных единиц в первой выборке X не превосходит a , то партию принять; если число дефектных единиц в первой выборке X больше или равно b, то партию забраковать; во всех остальных случаях, т.е. когда Х больше a, но меньше b, следует взять вторую выборку объема m; если число дефектных единиц во второй выборке Y не превосходит c, то партию принять, в противном случае забраковать.
Рассмотрим в качестве примера план (20, 0, 2) + (40, 0). Сначала берется первая выборка объема 20. Если все единицы в ней - годные, то партия принимается. Если две или больше - дефектные, партия бракуется. А если только одно - дефектное? В реальной ситуации в таких случаях начинаются споры между представителями предприятия и экологического контроля, или поставщика и потребителя. Говорят, например, что дефектная единица случайно попала в партию, что ее подсунули конкуренты или что при контроле случайно сделан неправильный вывод. Поэтому, чтобы споры пресечь, берут вторую выборку объема 40 (вдвое большего, чем в первый раз). Если все единицы во второй выборке - годные, то партию принимают, в противном случае - бракуют.
В реальной нормативно-технической документации - договорах на поставку, стандартах, технических условиях, инструкциях по экологическому контролю и т.д. - не всегда четко сформулированы планы статистического контроля и правила принятия решений. Например, при описании двухступенчатого плана контроля вместо задания приемочного числа с может стоять загадочная фраза "результат контроля второй выборки считается окончательным". Остается гадать, как принимать решение по второй выборке. Менеджер, администратор (государственный служащий), эколог или экономист, занимающийся вопросами экологического контроля или контроля качества, должен первым делам добиваться кристальной ясности в формулировках правил принятия решений, иначе ошибочные и необоснованные решения, а потому и убытки неизбежны.
Оперативная характеристика плана статистического контроля
Каковы свойства плана статистического контроля? Они, как правило, определяются с помощью функции f(p), связывающей вероятность p дефектности единицы контроля с вероятностью f(p) положительной оценки экологической обстановки (приемки партии) по результатам контроля. При этом вероятность p того, что конкретная единица дефектна, называется входным уровнем дефектности, а указанная функция называется оперативной характеристикой плана контроля. Если дефектные единицы отсутствуют, р = 0, то партия всегда принимается, т.е. f(0) = 1. Если все единицы дефектные, р = 1, то партия наверняка бракуется, f(1) = 0. Между этими крайними значениями р функция f(p) монотонно убывает.
Вычислим оперативную характеристику плана (n,0). Поскольку партия принимается тогда и только тогда, когда все единицы являются годными, а вероятность того, что конкретная единица—годная, равна (1‑р), то оперативная характеристика имеет вид
f(p) = Р(Х=0) = (1—р)n. (5)
Для плана (n,1) оперативная характеристика, как легко видеть, такова:
f(p) = Р(Х=0)+Р(Х=1) = (1—р)n + n (1—р)n-1 (6)
Оперативные характеристики для конкретных планов статистического контроля не всегда имеют такой простой вид, как в случае формул (5) и (6). Рассмотрим в качестве примера план (20, 0, 2) + (40, 0). Сначала найдем вероятность того, что партия будет принята по результатам контроля первой партии. Согласно формуле (5) имеем:
f1(p) = Р(Х=0) = (1—р)20.
Вероятность того, что понадобится контроль второй выборки, равна
Р(Х=1) = 20(1—р)19.
При этом вероятность того, что по результатам её контроля партия будет принята, равна
f2(p) = Р(Х=0) = (1—р)40.
Следовательно, вероятность того, что партия будет принята со второй попытки, т.е. что при контроле первой выборки обнаружится ровно одна дефектная единица, а затем при контроле второй—ни одной, равна
f3(p) = Р(Х=1) f2(p) = 20(1—р)19(1—р)40= 20(1—р)59.
Следовательно, вероятность принятия партии с первой или со второй попытки равна
f(p) = f1(p) + f3(p) = (1—р)20+ 20(1—р)59.
При практическом применении методов статистического приемочного контроля для нахождения оперативных характеристик планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы.
Риск поставщика и риск потребителя, приемочный и браковочный уровни дефектности
С оперативной характеристикой связаны важные понятия приемочного и браковочного уровней дефектности, а также понятия "риск поставщика" и "риск потребителя". Чтобы ввести эти понятия, на оперативной характеристике выделяют две характерные точки, делящие входные уровни дефектности на три зоны—А, Б и В. В зоне А все почти всегда хорошо, а именно - почти всегда обстановка признается благополучной, почти все партии принимаются. В зоне В, наоборот, почти всегда все плохо, а именно - почти всегда контроль констатирует нарушения, почти все партии бракуются. Зона. Б - буферная, переходная, промежуточная, в ней как вероятность приемки, так и вероятность браковки заметно отличаются от 0 и 1. Для задания границ между зонами выбирают два малых числа—риск поставщика (производителя, предприятия) α и риск потребителя (заказчика, системы экологического контроля) β, при этом границы между зонами задают два уровня дефектности - приемочный pпp и браковочный pбр, определяемые из уравнений
(7)
(7)
Таким образом, если входной уровень дефектности не превосходит pпp, то вероятность забракования партии мала, т.е. не превосходит α. Приемочный уровень дефектности выделяет зону А значений входного уровня дефектности, в которой нарушения экологической безопасности почти всегда не отмечаются, партии почти всегда принимаются, т.е. соблюдаются интересы проверяемого предприятия (в экологии), поставщика (при контроле качества). Это - зона комфортности для поставщика. Если он обеспечивает работу (уровень дефектности) в этой зоне, то его никто не потревожит.
Если же входной уровень дефектности больше браковочного уровня дефектности pбр, то нарушения почти наверняка фиксируются, партия почти всегда бракуется, т.е. экологи узнают о нарушениях, потребитель оказывается защищен от попадания к нему партий со столь высоким уровнем брака. Поэтому можно сказать, что в зоне В соблюдаются интересы потребителей - брак к ним не попадает.
При выборе плана контроля часто начинают с выбора приемочного и браковочного уровней дефектности. При этом выбор конкретного значения приемочного уровня дефектности отражает интересы поставщика, а выбор конкретного значения браковочного уровня дефектности - интересы потребителя. Можно доказать, что для любых положительных чисел β и α , и любых входных уровней дефектности pпp и pбр, причем pпp меньше pбр, найдется план контроля (n,c) такой, что его оперативная характеристика f(p) удовлетворяет неравенствам
При практических расчетах обычно принимают α = 0,05 (т.е. 5%) и β = 0,1 (т.е. 10%).
Можно определить приемочный и браковочный уровни дефектности для плана (n,0). Из формул (5) и (7) вытекает, что
Поскольку риск поставщика α мал, то из известного соотношения математического анализа
Для браковочного уровня дефектности имеем
При практическом применении методов статистического приемочного контроля для нахождения приемочных и браковочных уровней дефектности планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы, имеющиеся в нормативно-технической документации или научно-технических публикациях.
Предел среднего выходного уровня дефектности
В зависимости от ситуации судьба забракованной партии может быть разной. Партия может быть утилизирована. У партии может быть понижена сортность, и она может быть продана по более низкой цене (при этом результаты выборочного контроля будут использованы не для проверки того, что выдержан заданный уровень качества, а для оценки реального уровня качества). Партия продукции может быть подвергнута сплошному контролю. При сплошном контроле все дефектные изделия обнаруживаются и либо исправляются на месте, либо извлекаются из партии. В результате в партии остаются только годные изделия. Такая процедура называется "контроль с разбраковкой".
При среднем входном уровне дефектности р и применении контроля с разбраковкой с вероятностью f(p) партия принимается (и уровень дефектности в ней по-прежнему равен р) и с вероятностью (1- f(p)) бракуется и подвергается сплошному контролю, в результате чего к потребителю поступают только годные изделия. Следовательно, по формуле полной вероятности средний выходной уровень дефектности равен
f1(p)= pf(p) +0(1 - f(p)) = pf(p).
Средний выходной уровень дефектности f1(p) равен 0 при р=0 и р=1, положителен на интервале (0;1), а потому достигает на нем максимума, который в теории статистического контроля называется пределом среднего выходного уровня дефектности (сокращенно ПСВУД):
Пример. Рассмотрим план (n,0). Для него f(p) = (1 - p)n и f1(p) = p(1-p)n. Чтобы найти ПСВУД, надо приравнять 0 производную среднего выходного уровня дефектности по среднему входному уровню дефектности:
В полученном уравнении корень р = 1 соответствует минимуму, а не максимуму. Поскольку непрерывная функция на замкнутом отрезке достигает максимума, то максимум достигается при
Следовательно,
По выражению (8) могут быть проведены конкретные расчеты. Однако оно довольно громоздко. Его можно упростить, используя один замечательный предел из курса математического анализа, а именно:
Сравнивая соотношения (8) и (9), видим, что
Первая скобка равна 1/n, а вторая согласно соотношению (9) приближается к 0,368 при росте объема выборки. Поэтому получаем простую асимптотическую формулу
Для более сложных планов ПСВУД рассчитывают с помощью более или менее сложных компьютерных программ.
При рассмотрении основ статистического контроля в настоящем пункте расчетные формулы удалось получить лишь для простейших планов, в основном для планов вида (n,0). Если ослабить требования и рассчитывать не на точные формулы, а на асимптотические, при  , то можно справиться и с одноступенчатыми планами вида (n, c).
, то можно справиться и с одноступенчатыми планами вида (n, c).
 , то можно справиться и с одноступенчатыми планами вида (n, c).
, то можно справиться и с одноступенчатыми планами вида (n, c).Заключение
Идея статистического метода управления качеством в процессе производства состоит в том, чтобы время от времени проверять небольшие партии продукции штук, только что сошедших со станка. По результатам таких проверок судят о качестве наладки. Эти проверки осуществляются не слишком часто, чтобы не лихорадить переналадками оборудования производственный процесс, и не слишком редко, чтобы не пропустить момент его разладки. Далее результаты наблюдений наносятся на так называемые контрольные карты, которые позволяют судить, что следует предпринимать после каждой серии таких наблюдений прекращать работу для переналадки оборудования или же продолжить производственный процесс.
Если на ряде производств первичное произведение замеров параметров, определяющих качество продукции, допустимо и теперь оценивать вручную, то на других производствах оно уже требует заметного усовершенствования и перехода к автоматизации замеров и обработки результатов измерений. Дело в том, что во многих случаях приходится иметь дело с огромной скоростью технологических операций. Скорость настолько велика, что пока оператор производит измерение параметров отобранных изделий, автомат успевает изготовить сотни других изделий, а прокатный стан прокатать сотни метров продукции. В результате при ручном измерении оказывается, что запаздывает информация о наладке процесса, а вместе с ней и управляющее воздействие. Вот почему теперь предложены автоматы, которые замеряют необходимые параметры и сами выполняют математические операции, необходимые для управления качеством.
Методы приемочного контроля и статистические методы управления качеством оказались весьма эффективным средством упорядочения производства и экономии станочного времени, материалов, рабочей силы. Экономический эффект от использования этих методов исчисляется миллиардами рублей, долларов, марок и т.д.
Список литературы
· Статистические методы повышения качества. Перевод с японского. / Под ред. Х. Кумэ. - М.: Финансы и статистика, 1990
· Гнеденко Б. В., Курс теории вероятностей: Учебник – Изд 6 перераб и доп.- М.: Наукаб 1988
· Орлов А.И., Эконометрика: Учебник. М.: Издательство "Экзамен", 2002.

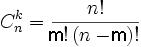













Комментариев нет:
Отправить комментарий